Выбор метрики качества в задачах прогнозирования спроса

Николай Курбатов, аналитик данных, Beltel Datanomics
При разработке систем прогнозирования товарных номенклатур (SKU) важным является выбор правильной метрики качества модели. Результат выбора непосредственным образом влияет на ценность решения.
В данной статье рассмотрим популярные метрики качества в задаче прогнозирования, их свойства, а также интерпретируемость, а также приведем примеры учета цены ошибки, которая для разных товаров может существенным образом отличаться. Покажем, как получить среднюю (интегральную) интерпретируемую оценку качества модели прогнозирования всех товаров с разными объемами продаж.
Метрики качества прогнозирования
Средняя абсолютная ошибка (MAE) и среднеквадратичная ошибка (RMSE) являются двумя наиболее распространенными показателями, используемыми для измерения точности в задаче прогнозирования спроса.
MAE измеряет среднюю величину ошибок в наборе прогнозов без учета их знака;

здесь горизонт прогнозирования начинается с до h, Yi, – фактическое значение продажи для определенного SKU, Fi– прогнозируемое значение продажи для этого SKU. Для задачи прогнозирования cпроса часто используют несимметричную модификацию метрики MAE [1].
RMSE – метрика симметричная относительно знака ошибки, чувствительная к большим отклонениям от среднего значения фактической величины продажи. Поэтому RMSE часто используют, когда хотят избежать больших ошибок в прогнозе:

MAE и RMSE выражают среднюю ошибку прогнозирования модели в единицах интересующей переменной. Обе метрики могут варьироваться от 0 до ∞ и безразличны к знаку ошибок; чем ниже эти метрики, тем более точные прогнозы мы получаем.
Проблема данных метрик в том, что они не интерпретируемы. Допустим, MAE для прогноза какой-то SKU равна 201.1. Непонятно много это или мало. Если сравнить метрики двух моделей, то станет ясно. Но сами по себе эти метрики не представляют ценности для оценки точности модели.
Как усреднять метрики?
1. Переход к относительным метрикам
Самое простое решение, когда нужно оценить качество модели на группе SKU – усреднить все метрики, посчитанные для отдельных товаров. Минус подхода в том, что позиции могут сильно различаться по объему продаж, соответственно будут отличаться и метрики. Чтобы избежать этого, нужно перейти к относительным метрикам перед усреднением. Существует несколько методов как это сделать:
- делить на фактическое значение продажи (MAPE):
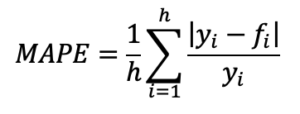
Эту относительную метрику просто интерпретировать, если перевести в проценты. Например, если MAPE = 1.5%, то это говорит о том, что ошибка составила 1.5% от фактических значений.
Минус MAPE в том, что она не определена в случае нулевого спроса, поэтому ее нельзя использовать для прогнозирования прерывистого спроса.
- делить на среднюю историческую продажу:

здесь ȳ – средняя историческая продажа для определенного SKU. Эта метрика также просто интерпретируема в процентах: history scaled MAE = 1.5%, говорит о том, что ошибка составила 1.5% от средней исторической продажи.
Плюс этой метрики в том, что она не может быть бесконечно большой, как MAPE.
Минус в том, что данный подход может привести к смещению нормировки при вычислении исторических средних значений для товаров с ярко выраженной сезонностью.
- делить на среднее прогноза и факта (SMAPE):

В случае когда Yi = Fi = 0, SMAPE = 0.
Данная метрика лишена недостатков двух предыдущих. Но SMAPE не симметрична, так как заниженные прогнозы штрафуются больше чем завышенные.
Все описанные методы перехода к относительным ошибкам можно применять и к другим метрикам, не только к MAE.
2. Взвешивание метрик
После нормирования метрик осталась еще одна проблема: в обычном усреднении мы присваиваем ошибке для каждого SKU одинаковый вес. Рассмотрим два товара: первый с большим объемом продаж и высокой стоимостью; второй с небольшим объемом и низкой стоимостью. В данном случае важнее достигнуть меньшей относительной метрики для первого продукта. Поэтому мы должны взвесить относительные показатели, чтобы учесть важность продуктов и общие объемы продаж.
Один из способов сделать это – взвесить каждый артикул на основе исторических объемов спроса:

где n – кол-во SKU, Wj – вес для j-го SKU (отношение объема исторических продаж j-го SKU на суммарный объем исторических продаж по всем SKU), (scaled error) j – относительная ошибка прогноза для j-го SKU.
Заключение
Стоит отметить, что для интерпретируемой и корректной оценки качества прогнозов для некоторого набора SKU недостаточно провести обычное усреднение метрик MAE и RMSE. Наиболее подходящими метриками для данной задачи являются средневзвешенные относительные MAE и RMSE. Также рекомендуется использовать набор метрик для принятия более обоснованных решений.
Список литературы
[1] http://www.machinelearning.ru/wiki/images/6/6d/Voron-ML-1.pdf